7714. Фрезерные станки

 

Fab-лаборатория — это небольшая открытая мастерская, где можно создать или изготовить практически всё, что угодно, в основном с помощью инструментов с компьютерным управлением, таких как лазерный резак или 3D-принтер. Недавно фаблаб FAU получил фрезерный станок с ЧПУ. С его помощью можно вырезать или снимать материал с поверхности заготовки различными инструментами. Управление осуществляется компьютерной программой.

Иногда мне становилось интересно, что произойдёт, если несколько заготовок разной формы обработать одной и той же программой фрезерования. Для упрощения предположим, что у нас есть только двумерные заготовки без отверстий. Программа фрезерования состоит из нескольких шагов, каждый из которых описывает, с каких участков поверхности фрезерный станок должен снять материал (с помощью различных инструментов).

 

Вход. Первая строка содержит два целых числа w и s (1 ≤ w, s ≤ 104) –  количество заготовок и количество шагов в программе фрезерования.

Следующая строка содержит два целых числа x и y (1 ≤ x, y ≤ 100), где x – ширина заготовки, а y – её максимально возможная высота.

Каждая из следующих w строк описывает одну заготовку. Описание каждой заготовки состоит из  неотрицательных целых чисел, задающих высоту поверхности в каждом столбце.

Далее следуют s строк, описывающих шаги фрезерования. Каждый шаг программы состоит из x неотрицательных целых чисел si (0 ≤ si ≤ y), определяющих, сколько материала нужно снять в каждом столбце (относительно высоты области фрезерования, то есть относительно y, а не верха заготовки). См. иллюстрацию.

 

Выход. Для каждой заготовки выведите одну строку, содержащую x целых чисел – оставшуюся высоту поверхности после всех шагов фрезерования (в том же порядке, что и во входных данных).

 

Рисунок. В первом примере показано, как выглядит вторая заготовка после последовательного применения всех шагов фрезерования: каждое значение в программе определяет вертикальное положение фрезерной головки.

 

 

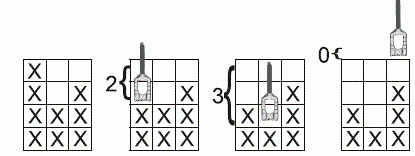
Пример входа 1

Пример выхода 1

2 1

3 4

4 4 4

4 2 3

2 3 0

2 1 4

2 1 3

 

 

Пример входа 2

Пример выхода 2

1 3

10 100

11 22 33 44 55 66 77 88 99 100

1 100 1 100 1 100 1 100 1 100

58 58 58 58 58 58 58 58 58 58

42 42 42 42 42 42 42 42 66 42

11 0 33 0 42 0 42 0 34 0

 

 

РЕШЕНИЕ

математика

 

Анализ алгоритма

Программа фрезерования состоит из s шагов. Пусть на i-ом (1 ≤ i ≤ s) шаге от поверхности в столбце j (1 ≤ j ≤ x) срезается слой толщиной mij. Тогда очевидно, что суммарно в столбце j будет снято

max(m1j, m2j, …, msj)

Схемой фрезерования будем называть набор целых чисел

(cuts1, cuts2, …, cutsx),

где

cutsj = max(m1j, m2j, …, msj), 1 ≤ j ≤ x

 

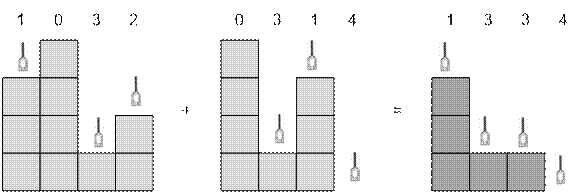
Одна и та же схема фрезерования применяется ко всем w деталям. После вычисления значений cutsj (1 ≤ j ≤ x) эту схему последовательно применяем к каждой детали.

 

Реализация алгоритма

Объявим рабочие массивы. Информацию о деталях будем хранить в массиве detail, а схему фрезерования – в массиве cuts.

 

int detail[10001][101], cuts[101];

 

Читаем входные данные.

 

scanf("%d %d %d %d", &w, &s, &x, &y);

 

Читаем информацию о w деталях.

 

for (i = 0; i < w; i++)

for (j = 0; j < x; j++)

  scanf("%d", &detail[i][j]);

 

Читаем и обрабатываем s шагов программы фрезерования. Для каждой позиции j значение cuts[j] будет обозначать максимальную глубину выреза, выполненного на каком-либо шаге.

 

for (i = 0; i < s; i++)

for (j = 0; j < x; j++)

{

  scanf("%d", &val);

  if (val > cuts[j]) cuts[j] = val;

}

 

Максимально возможная высота заготовки равна y. Фрезерная головка в позиции j опускается на глубину cuts[j]. Следовательно, после фрезерования в позиции j у i-й детали останется высота, равная

min(detail[i][j], y – cuts[j]).

 

for (i = 0; i < w; i++)

{

  for (j = 0; j < x; j++)

    printf("%d ", min(detail[i][j], y - cuts[j]));

  printf("\n");

}